2023成都中考数学解析(部分)
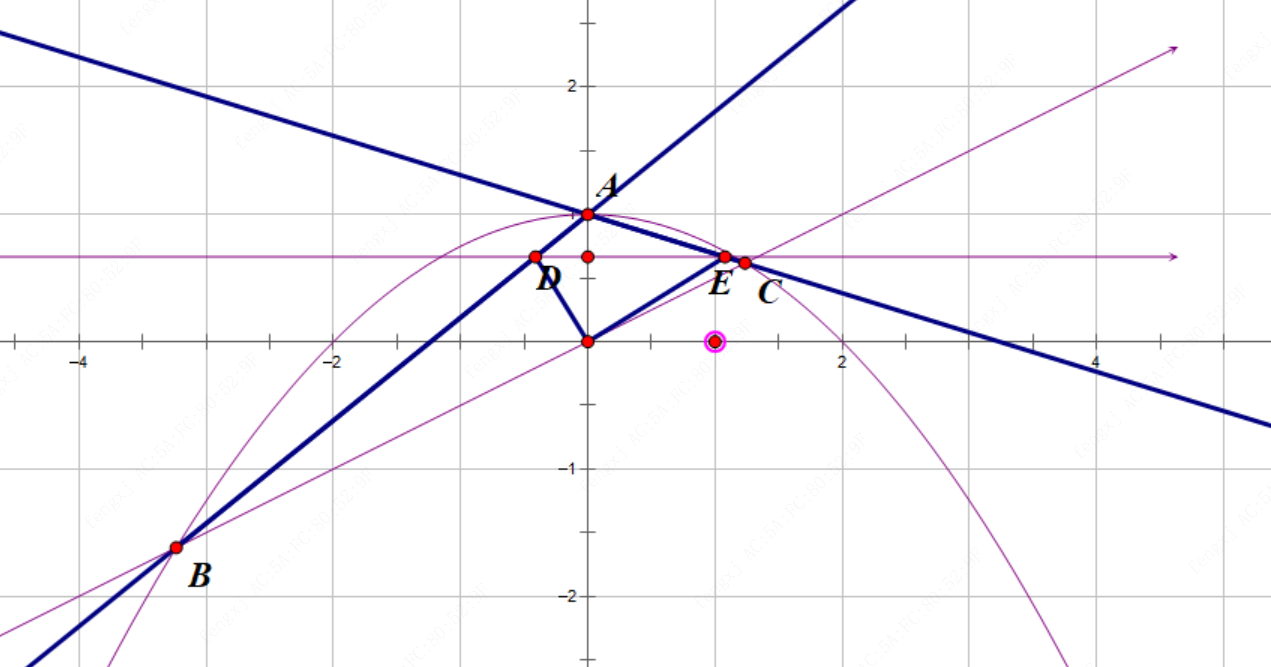
22.如图,在 $Rt \Delta ABC$ 中,$∠ABC=90°$ , $CD$ 平分 $∠ACB$ 交 $AB$ 于点 $D$ ,过$D$ 作 $DE//BC$ 交 $AC$ 于点 $E$ , 将 $\Delta DEC$ 沿 $DE$ 折叠得到 $\Delta DEF$ , $DF$ 交 $AC$ 于点 $G$ ,若 $\frac{AG}{GE}=\frac{7}{3}$ ,求 $tanA$.
解析:利用相似找到边的比例关系。说白了就是一道解三角形的问题,比较简单。思路可能稍微有点思维含量,但计算难度是一点没有。
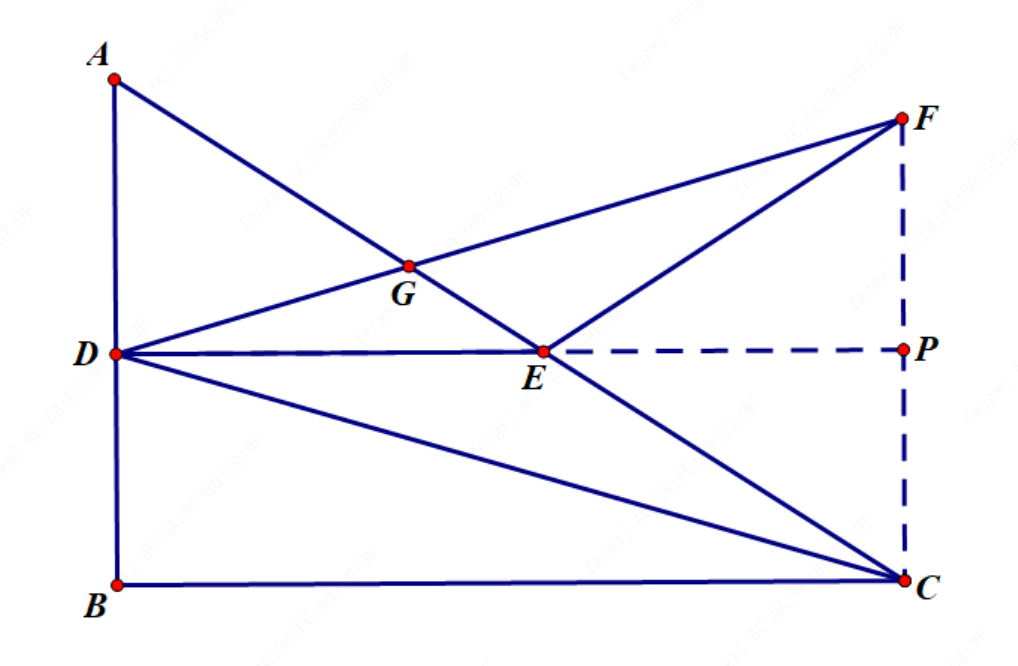
解法:连接 $FP$ , 延长 $DE$ 交 $FC$ 与点 $P$.
设 $AG=7,GE=3,CE=a$.
易证: $\Delta AGD \sim \Delta CGF$
$\therefore \frac{AD}{FC}=\frac{AG}{GE}=\frac{7}{3+a}$ .
易证: $\Delta DFP \cong \Delta DCP$ 且 $DBPC$ 为矩形
$\therefore DB // FC$ 且 $DB = \frac12 FC$
故 $\frac{AD}{DB}=\frac{14}{3+a}$
由平行线分线段成比例定理得: $\frac{AD}{DB}=\frac{AE}{EC}=\frac{10}{a}=\frac{14}{3+a}$
解得 $a=\frac{15}{2}$
$\because DE//BC$ 且 $\angle ECD = \angle DCB$
$\therefore DE=EC=a=\frac{15}2$
在 $\Delta ADE$ 中,由勾股定理:
$AD=\sqrt{AE^2-DE^2}=\sqrt{10^2-(\frac{15}2)^2}=\frac52 \sqrt7$
$\therefore \tan A= \frac{DE}{AD}=\frac{3\sqrt7}7$
23.定义:如果一个正整数能表示为两个正整数 $m,n$ 的平方差,且 $m-n> 1$ ,则称这个正整数为“智慧优数”.例如, $16=5^2-3^2$ ,$16$ 就是一一个智慧优数,可以利用 $m^2-n^2 =(m+n) (m-n)$ 进行研究.若将智慧优数从小到大排列,求第3个和第23个智慧优数.
解析: 没想到今年的B填压轴居然是一道数论题。貌似今年没有考动点的最值问题,这与去年的那道23题还是有很大的差距的。这道题的思维含量还是可以的,考场上遇到这种题反正我是不会有什么思路的。其实这道题的思路都是枚举,只不过是不同的枚举方式罢了。第一问是很好枚举的,但第二问需要找一些规律。总之,这里提供一种可行的解法。
解法:$Solution1:$ 筛法.
我们先设 $m^2-n^2=x$ .
我们可以枚举 $m$ 和 $n$ 的差值,即 $i=m-n,i \geq 2$ .
变形可得 $m=i+n$ ,将 $m$ 代入,$x=2in+i^2$
我们可以设 $f_i(n)=2in+i^2$ ,那么问题就转化为求 $f_i(n)$ 的值从小到大的排序.
先举个例子,当 $i=2$ 时 ,$f_2(n)=8,12,16,20,24\dots$
当 $i=3$ 时 ,$f_3(n)=15,24,33,42,51\dots$
当 $i=4$ 时,$f_4(n)=24,40,56,72,88,104\dots$
我们会发现,这不就是一个筛法吗?
筛法的概念和简介可以看这篇文章 。
所以我们可以只用枚举 $i=2,3,5$ 的情况。当我们枚举到 $i=7$ 时会发现 $f_7(1)$ 已经大于当前的最大数,所以可以停止枚举。
- 如图,在平面直角坐标系 $xOy$ 中,已知抛物线 $y=ax^2+c$ 经过点 $P(4,-3)$ ,与y轴交于点 $A(0, 1)$ ,直线$y=kx(k≠0)$ 与抛物线交于 $B,C$ 两点.
(1)求抛物线的函数表达式;
(2)若 $\Delta ABP$ 是以 $AB$ 为腰的等腰三角形,求点 $B$ 的坐标;
(3)过点 $M(0,m)$ 作 $y$ 轴的垂线,交直线 $AB$ 于点 $D$ ,交直线 $AC$ 于点 $E$ .试探究: 是否存在常数 $m$ ,使得$OD⊥OE$ 始终成立?若存在,求出 $m$ 的值;若不存在,请说明理由.
解析:一道比较常规的二次函数题,没有什么技术含量。第二问为一个比较简单的三角形存在性问题。第三问直接代值暴力计算即刻。只是计算量有点小大,考场上可能比较容易算错。
解法:(1) 将点 $P(4,-3),A(0,1)$ 代入抛物线 $y=ax^2+c$:
解得:
故抛物线的解析式为 $y=-\frac14x^2+1$
(2) $Case 1:$ $AP$ 、$AB$ 为等腰三角形的腰, $BP$ 为底边.
则 $B$ 为 $P$ 关于 $y$ 轴的对称点, $B$ 点坐标为 $(-4,-3)$.
$Case 2:$ $BP$ 、$AB$ 为等腰三角形的腰, $AP$ 为底边.
则 $B$ 在直线 $AP$ 的中垂线与抛物线的交点处.
由题可得:$k_{AP}=-1$ , $l_{AP}=-x+1$ .
则 $l_{AP}$ 的中垂线为 $l_1=x-3$
联立直线 $l_1$ 和 抛物线 $y$ 得:
解得: $x=-2-2\sqrt5$ 或 $-2+2\sqrt{5}$
则 $B$ 的坐标为 $(-2-2\sqrt5,-5-2\sqrt5)$ 或 $(-2+2\sqrt5,-5+2\sqrt{5})$
综上所述:$B$ 的坐标为$(-4,-3)$ , $(-2-2\sqrt5,-5-2\sqrt5)$ 或 $(-2+2\sqrt5,-5+2\sqrt{5})$.
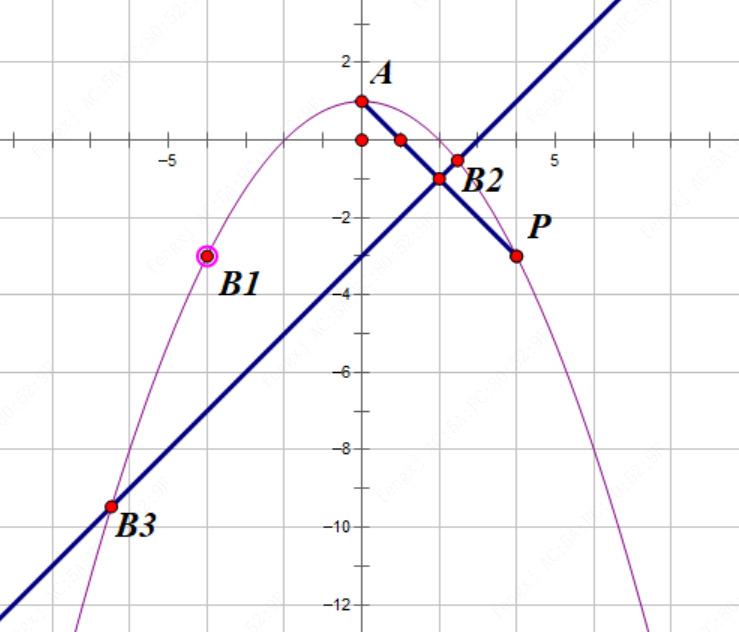
(3) 存在 $m=2$ 或 $\frac23$ 使得题目条件成立.
设 $B$ 在 $x$ 轴负半轴,$C$ 在 $x$ 轴正半轴.
已知 $l_{BC}=kx$ ,联立 $l_{BC}$ 和抛物线 $y$ :
解得: $B(-2k-\sqrt{4k^2+4},-2k^2-k\sqrt{4k^2+4}),C(-2k+\sqrt{4k^2+4},-2k^2+k\sqrt{4k^2+4})$ .
令 $\varphi_1=-2k-\sqrt{4k^2+4},-2k^2-k\sqrt{4k^2+4},\varphi_2=-2k+\sqrt{4k^2+4},-2k^2+k\sqrt{4k^2+4}$ .
则 $B(\varphi_1,k\varphi_1),C(\varphi_2,k\varphi_2)$ .
设 $l_{AB}=kx+b$, 将 $A(0,1),B(\varphi_1,k\varphi_1)$ 代入,解得 $l_{BC}=\frac{k\varphi_1-1}{\varphi_1}x+1$
当 $y=m$ 时, $m=\frac{k\varphi_1-1}{\varphi_1}x+1$
解得 $x=\frac{\varphi_1(m-1)}{k\varphi_1-1}$ , $D(\frac{\varphi_1(m-1)}{k\varphi_1-1},m)$ .
同理可得,$E(\frac{\varphi_2(m-1)}{k\varphi_2-1},m)$ .
若 $OD⊥OE$ , 则有
整理得
将 $\varphi_1=-2k-\sqrt{4k^2+4},-2k^2-k\sqrt{4k^2+4},\varphi_2=-2k+\sqrt{4k^2+4},-2k^2+k\sqrt{4k^2+4}$ 代入方程
有 $-4(m-1)^2=m^2$
解得 $m=2$ 或 $\frac23$